3n + 1

The Collatz Conjecture, or the 3n + 1 problem, is an infamous and (at time of writing) unproven conjecture. First proposed (maybe) when Lothar Collatz conjectured that for all natural numbers \(N\), running the following procedure will eventually result in the interminable 4-2-1 cycle:

function collatz(n):
    if n % 2 == 0:
        return collatz(n/2)
    else:
        return collatz(3n+1)

In plain english, this means: Pick a number. If it’s even, divide it by two. If it’s odd, mutliply it by 3 and add 1. Repeat this process forever. The conjecture is that no matter what number you begin with, you’ll wind up in a loop of 4-2-1. The reason we call it the 3n + 1 problem is because we can not prove that this statement is actually true. It’s easy to see that we reach this cycle for any number that we check- and mathematicians have checked an incomprehensibly large amount of positive integers (up to ~2.39e21 at time of writing), but none have proven the statement.

Now why am I, a computer scientist, wasting any amount of time on this? Well, I’m not… anymore, anyways. But a while back, sometime during my undergraduate degree, I was very interested in this problem. I wanted to understand what all these geniuses say we can’t understand: Does the conjecture hold for all n? Can we prove it?

In the end I was unable to prove anything of any significance whatsoever. This was expected, me not being a once-in-a-generation number theorist. But my pattern-seeking brain did notice a something in the path-trace “tree” produced by the 3n + 1 process. I say “tree” because the graph produced by the collatz process does in fact have at least one cycle (real trees are acyclic by definition); the 4-2-1 loop. Here is an illustration of that graph, showing all paths that take \(\leq\) 7 steps to reach the cycle:

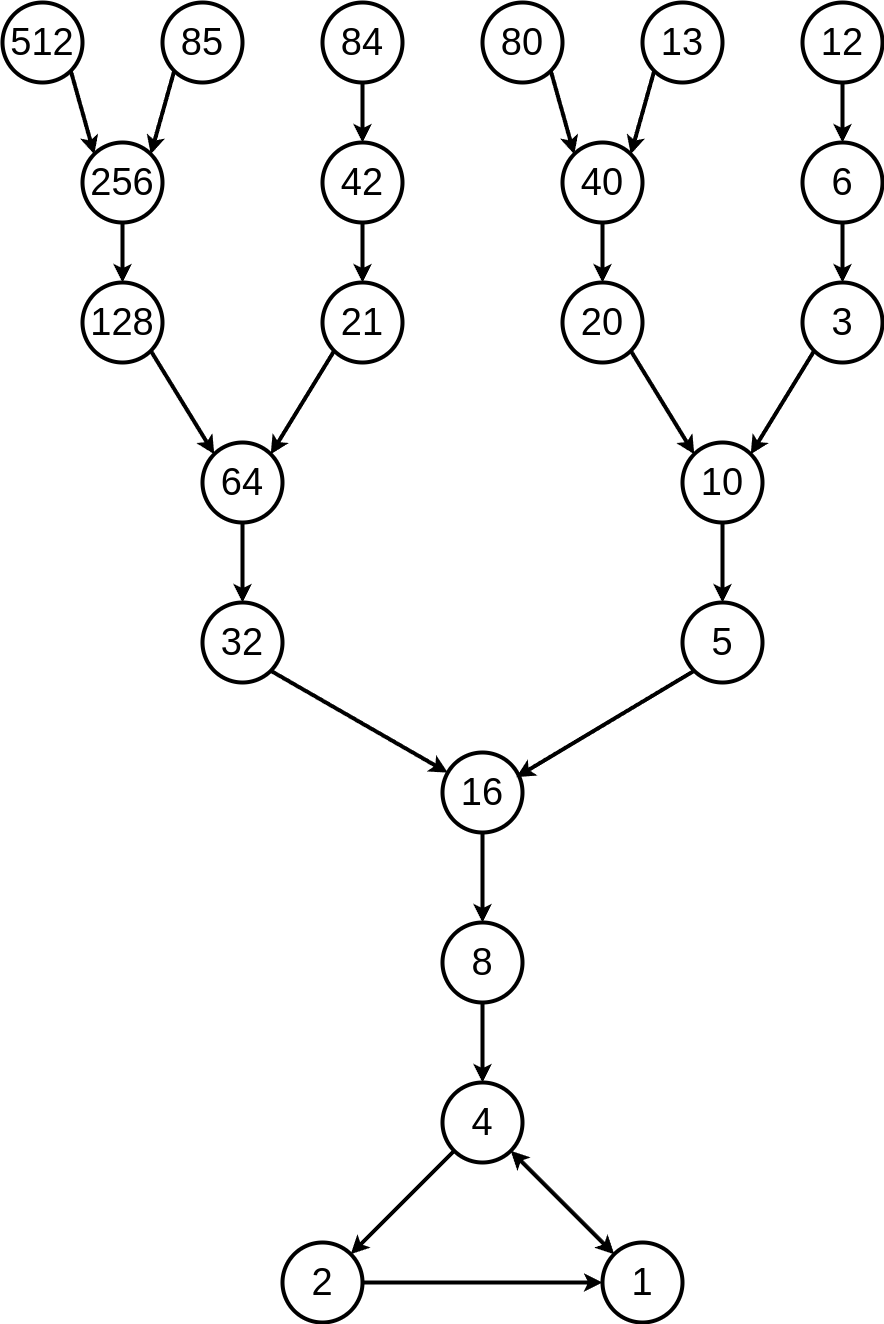
So, not quite a tree. Before I proceed with my delirious rant, there are few notes about my terminology and about this graph (assuming the Collatz conjecture is true):

1. The 4-2-1 cycle is the only cycle in the graph.
2. Every natural number appears in the graph exactly once.
3. All numbers \(N\) in the graph have at least one parent \(2N\). I refer to this as the even parent
4. Some numbers \(N\) in the graph may have one additional parent (the odd parent), if \(\frac{(N-1)}{3} \bmod 2 = 1\). I refer to these as split numbers.
5. For all \(N\) with two parents, the even parent is always greater than the odd parent (obviously: \(2N > \frac{(N-1)}{3} \ \forall N \in \mathbb{N}\))

But what about that pattern I mentioned? Well, in order to see this pattern, first note the “split” numbers- those numbers \(N\) in the graph which have two parents, shown here in red:



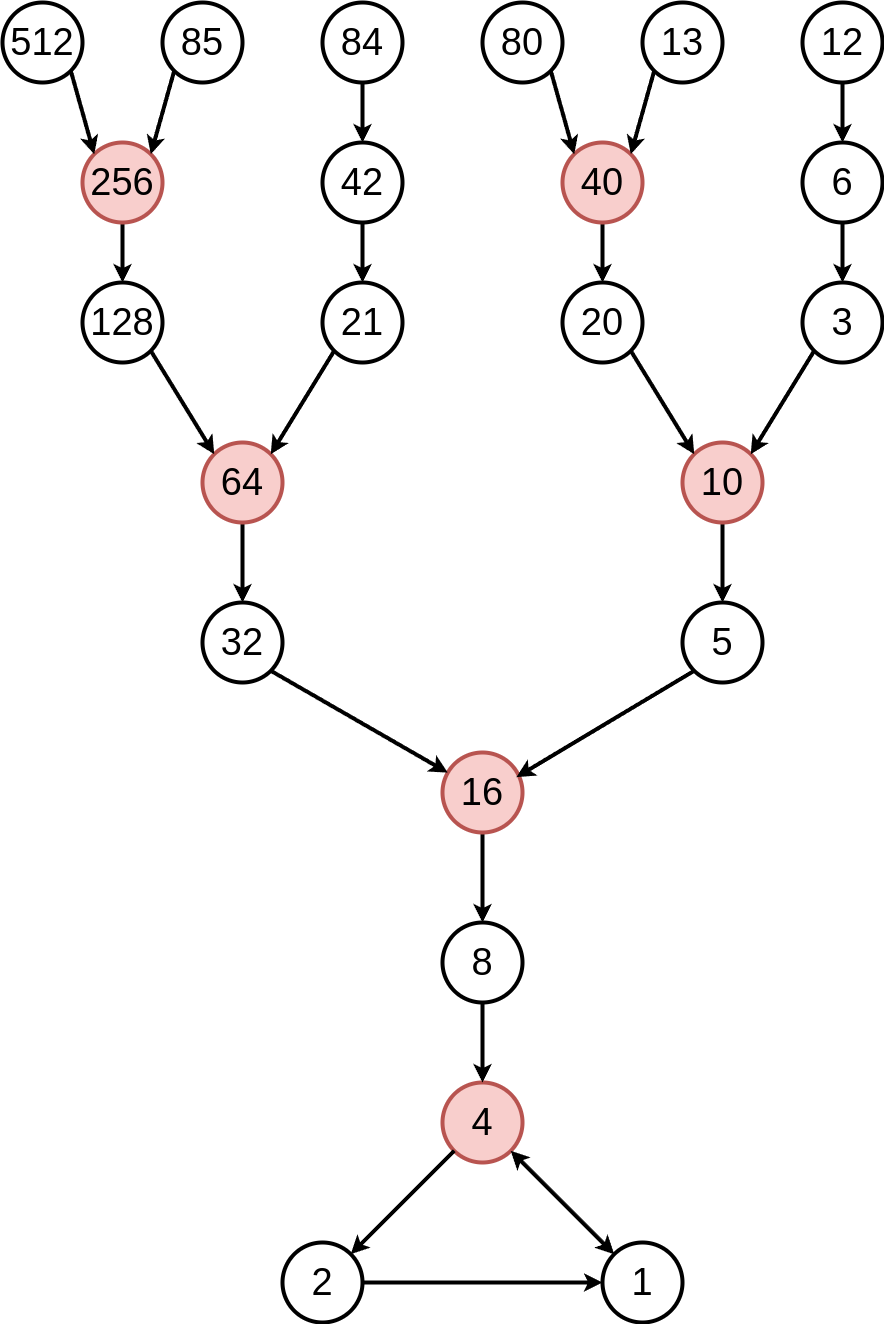
Now this is where we make our first blind leap. For each split number, take the difference between the even parent (in blue) and the odd parent (in green). This difference is shown in red:



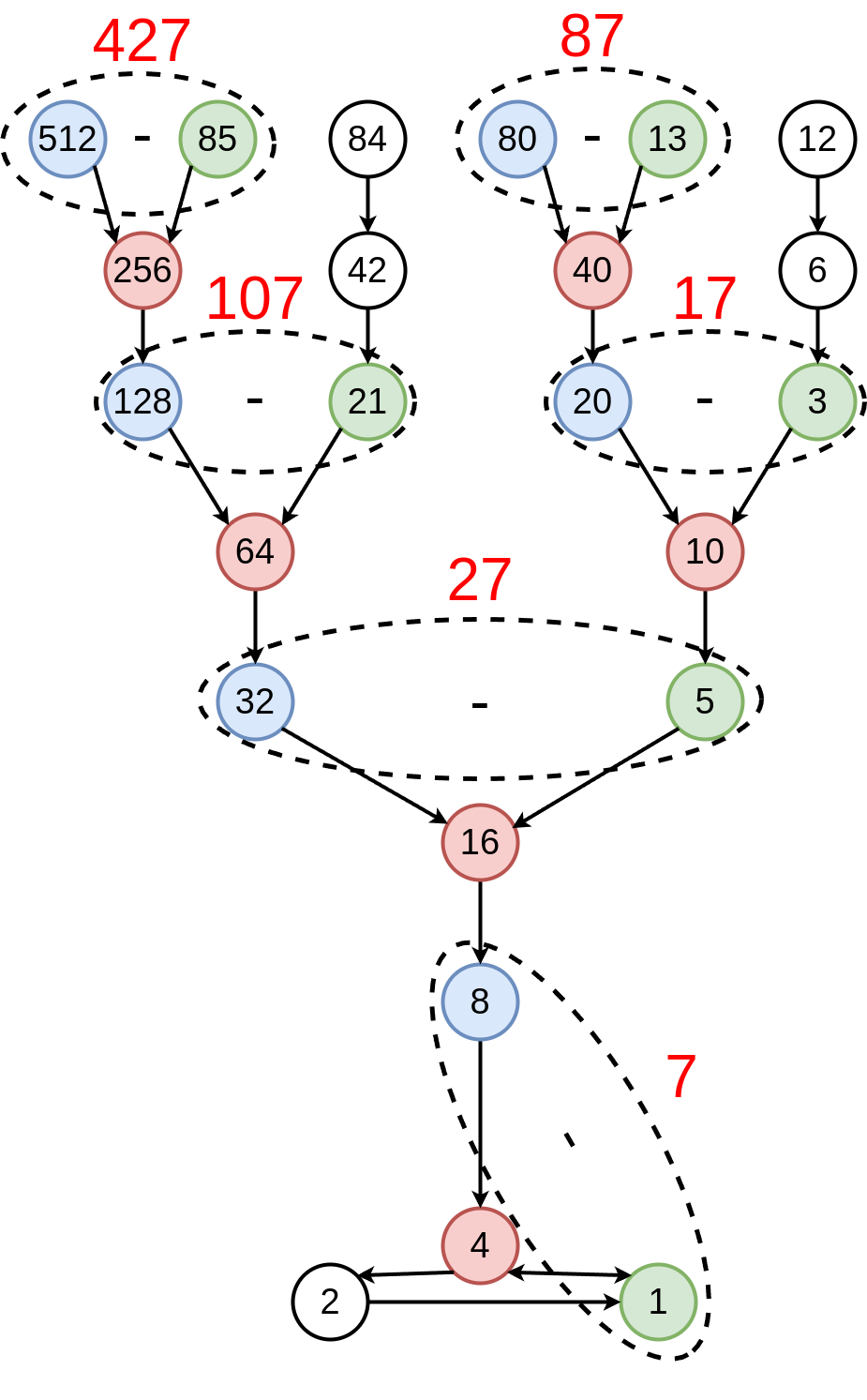
Splendid. we’ve done a bunch of arbitrary operations, yielding no interesting result whatsoever. Except , a brief inspection of these values reveals one common feature: they all end in 7. This was the first thing that I noticed after considering the difference-of-parents operation. This alone was exciting to me, as I had no intuition as to why this procedure always yields a number that ends in 7. After writing a script to draw this graph up to arbitrary depths, I noticed a second feature shared by all of these differences: their prefix is equal to the neighbor of their split number.



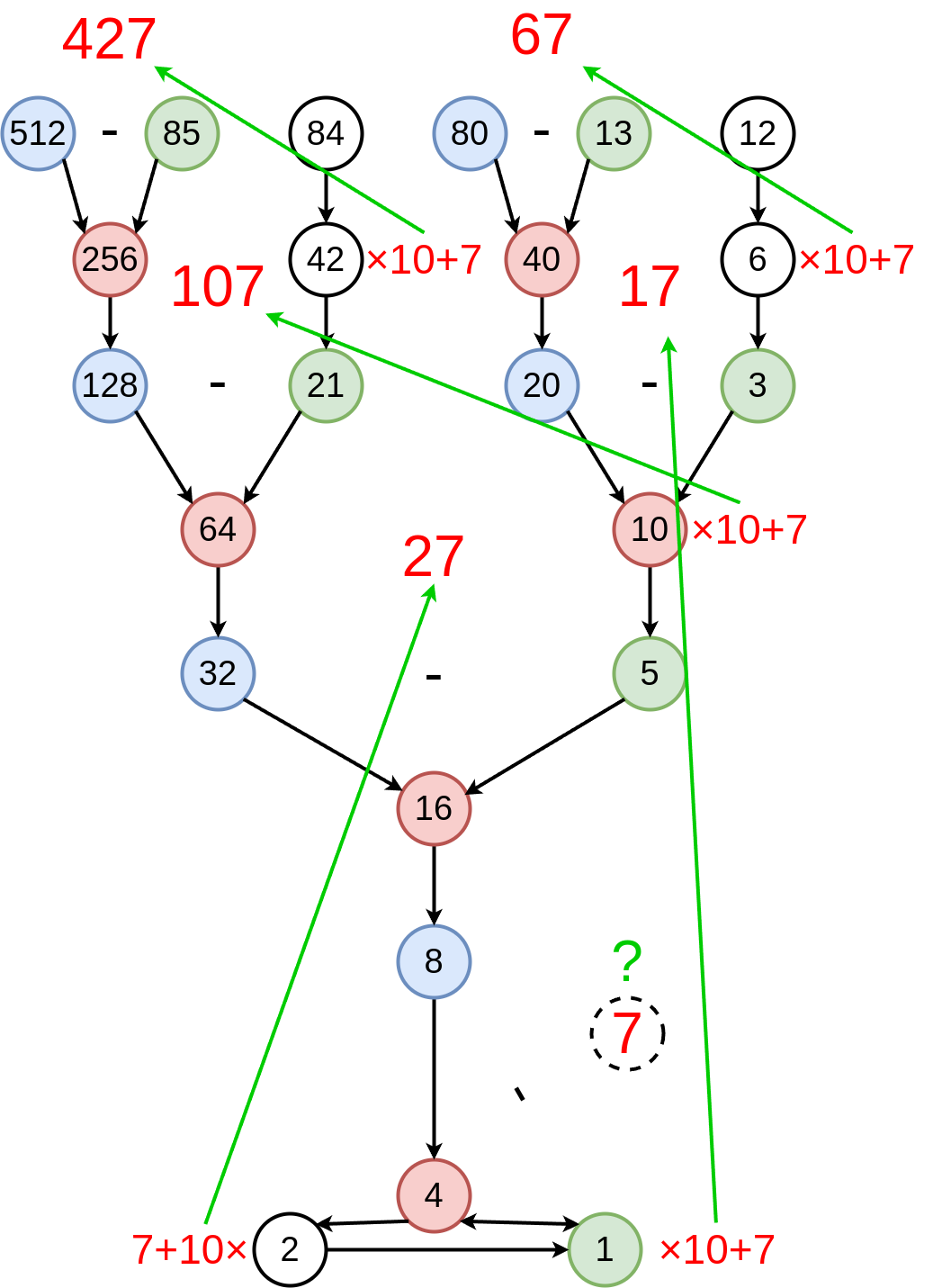
Now that I’ve made my figure pretty much indecipherable, I will go through an example of what I’m talking about. Take the split number 256 for example. Its even parent is 512 and its odd parent is 85. Their difference is 427. The neighbor of the split number 256 is 42. 42 is the “prefix” of 427. Follow this logic for the other split numbers in the figure (40, 64, 10, 16, and 4) and you will find that this pattern seems to hold. Which is neat! But testing this for a bunch of numbers proves nothing. And what about that singular 7? My logic is telling me “The split number 4 has parents 8 and 1, their difference is 7, which is 10 times 0 plus 7. 0 must be the neighbor of the split node 4”, even though this can not be, as 0 is not a natural number; it is not even nor odd and does not appear on the graph. So what is really going on here? In order to understand the mechanics of the pattern at play, I conduct a brief algebraic exercise, including a more formal description and proof of my so-called pattern.

First, I define the difference between the even and odd parents of a split number \(N\):

Then, I define the neighbor of the split numbers:

My claim is that the difference between its even and odd parent is equal to 10 times the neighbor of \(N\) plus 7:

An infant bonobo could prove this claim with simple algebra:

Voila. Not only is the claim true for the split numbers (a small set of natural numbers), but in fact it is true for \(N \in \mathbb{R}\)! This mental exercise has no point or purpose but to provide some insight into why the Collatz Conjecture has captivated so many minds over the years. Its simple premise is so easily understood, its many patterns are so readily perceptible. Many human geniuses (including Terence Tao) have set out to prove or disprove the conjecture once and for all, but none have succeeded. Burgeoning mathematicians are discouraged from investigating it, lest they exhaust their time and sanity and end up wasting their potential. Wise as this advice may be, there will always be curious apes who aren’t intimidated by unsolveable problems, and who desire above all else to explore the limits of our collective knowledge. I believe that humanity (or its progeny) will one day produce such an individual, who possesses the wit and ingenuity to give us the answer, and that this answer will betray the hidden beauty of mathematics, observable to us in the form of Euler’s Identity, general relativity, Lie Groups, and more.

If you made it this far, I sincerely thank you for putting in the effort. I want to conclude this post by recalling the legend of the Gordian Knot- the knot which could not be untied. All efforts to untie this knot failed, and these many failures only added to its infamy. An oracle professed that the man who succeeded in untying the knot would come to rule all of Asia. Finally, one aspirant succeeded. It’s said that Alexander the Great approached the knot and sliced it with his sword. His solution to the problem was, in fact, a re-definition of the problem itself. A natural course of action; one questions the unanswerable question. It may be that such an approach will be necessary as we continue our search for the truth of the Collatz Conjecture.